Pages: << 1 ... 10 11 12 13 14 15 16 17 18 19 20 ... 59 >>
2020/05/16
海流と木星
海流に電流が流れていることは19世紀ごろから知られていたらしい。現在では地球磁場を横切る海流が電磁誘導で電流を発生させていると考えられている。しかし、これは逆のような気がする。海水に電流が流れ込んでいるため、地球磁場との関係で海流が生まれ、磁場が発生していると電気的地球科学では考える。海流の実際の流れを見てほしい。

蛇行する黒潮の両側に丸い渦があることがわかる。丸い渦は磁場の周囲に現れる円電流だ。同じパターンが木星の表面にも見ることができる。

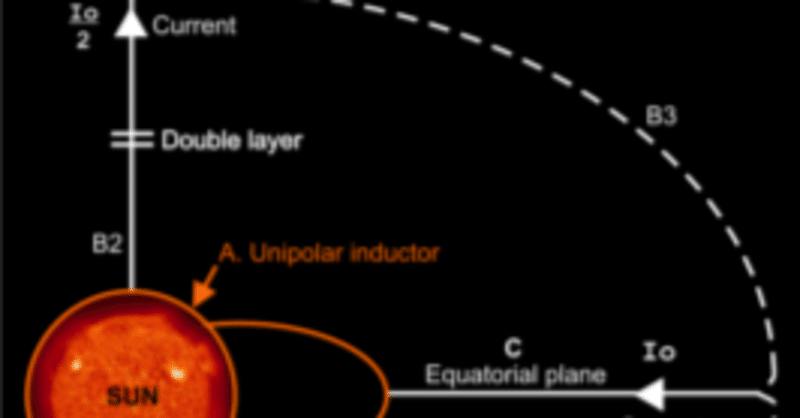
木星大気はプラズマでその流れは電流だからだ。木星は自前のエネルギーで活動しているのではない。かつて太陽だった木星にはいまでも銀河風の星間物質が流入している。太陽に入る星間物質を横取りしているのだ。そのため、土星、木星の位置が太陽よりも銀河の進行方向に対して、前方に位置すると太陽活動が低下することになる。木星、土星に入る星間物質が多くなるからだ。
ところで、木星内部の構造はどうなっているのだろう? 太陽だった時に融合されたシリコン、酸素、鉄などが大量にあるはずだが、それらはコアのように一つにまとまってはいないだろう。代表的な岩石成分であるSiO6はバラバラに木星内部にあるはずだ。マイナスの電荷をもつので互いに反発するからだ。

プラズマ大気の中では低温核融合が進んでいく。太陽磁場の影響が地球よりもはるかに少ないので、木星大気には銀河由来の高エネルギー宇宙線が大量に降り注いでくる。大量のニュートリノが発生しているはずだ。ニュートリノは木星大気の成分である水素、メタンをより重い元素に変換していく。プラズマ大気の下層は電流のため高温かもしれない。圧力は高くないはずだ。木星はプラズマ大気が静電モーターで回転しているため、少し扁平になっている。木星を球形に保っている力は、内部のマイナスの岩石がプラスの大気を引き付けているだけではないだろう。木星の自転速度は10時間と岩石惑星より圧倒的に速いからだ。回転するプラズマは強力な磁場を発生させている。同時に地球と同じように超低周波の電磁波を発生させているはずだ。電磁質量の発生が木星を球形に維持しているのだ。
木星にも地球と同じように電離層が存在する。電磁質量を一定に保つメカニズムもあると考えられる。
2020/04/25
放電には3種類ある
月刊ムー2020年3月号の特集記事では地球の地形がどのようにしてできたかを説明している。紙面の都合上、詳しく説明できなかった個所を補ってみたい。これまで惑星規模の放電が地形を形成してきたと説明したが、具体的にどのようにして地形が出来たかは触れないで来た。
電気溶接を例に取ると放電には3種類ある。巨大な惑星間の放電と電気溶接は無関係と思うかもしれないが、プラズマによる現象はスケールが違ってもパターンは共通している。

電気溶接は大きく分けると直流と交流がある。惑星間の放電は大方直流であると考えられる。惑星双方の岩石に蓄えられた電荷が電流源だからだ。電荷の電位差が放電の原因になる。直流放電では、プラスとマイナスの違いが大きい。たとえば、溶接棒がマイナスの場合、金属は溶接棒から母材(溶接する金属)に大きく移動する。また母材の奥深くに電流が流れ込むので溶ける深さが深くなる。要は溶ける面積は狭いが深く溶けて金属が大量に母材側に移動する。逆に溶接棒がプラスで母材がマイナスの場合、溶ける範囲は広がるが深さは浅い。移動する金属も少ない。
この極性の違いは惑星では生じる山とクレーターの違いとして現れる。火星の半分はクレーターが多い。マイナス側として放電したためだ。

プラス側になって放電すると山ができる。火星のオリンポス山などが該当する(しかし、後で解説するがこれには疑問もある)。

電気溶接には、磁気吹きという現象が起きることが知られている。放電が自らの磁場で曲がるのだ。

日本列島の山には磁気吹きが作ったと思える地形が残っている。しかし、火星のオリンポス山などの山には、この地形が存在しない。大気が薄いせいだという説明もできるが、大室山そっくりの地形もあるので、オリンポス山の形成には、放電だけではない要素があると考えている。

赤色地形図で見ると日本列島はひだのような地形でおおわれている。噴火口のない山は、隆起した土地が長い間の浸食で作られたとされる。しかし、このブログでも指摘したように浸食されて流れたはずの土砂はどこにもないのだ。

地表を覆う山々は、地球がプラス側として放電を受けたために形成された、電気溶接でのスラグということになる。これは岩石に塩基性成分が多いことが示している。溶接スラグもアルカリ性、塩基性の成分でできている。月の岩石が地球と同じ成分であるのは、月がマイナスのため、月の表面の岩石が放電のスラグとして地球に降り注いだからだ。
私たちが日ごろ目にしている山は、放電によってあっという間に作られたのだ。
2020/04/21
オルタナティブフィジックス②
前回の続きで、磁場を解説している。磁力線が個々の荷電粒子から発生する円形磁場のベクトルが合成されたものであることを踏まえて読むと理解がよく出来る。
磁場の正しい表現
先に進む前のいくつかの最後のポイント。磁力線の一般的な誤表示を修正したいと思います。磁場は、ワイヤーを取り巻くように描かれます。このような図は次のようになります。

この図では、磁力線はワイヤーからさまざまな距離で始まり、固定された半径で円を描くように進んでいるように見えます。また、通常、図の横に手の写真が含まれており(含まれていません)、右手の法則について説明するための「いいね」を示しています。この図の意味するところは、磁力が直角に作用し、ワイヤーを円周するように強制することです。
しかし、これは明らかに正しくありません。2本の通電ワイヤが平行に配置されている場合、それらの間の唯一の力は、互いに直接近づくか、または互いに離れるだけです。図が示すように、ワイヤーがお互いを周回するかのように、ワイヤーが横に押されることはありません。彼らもそうではありませんでした。力が発生した場合で、ワイヤ、その力が来なければならないから そのワイヤー。言い換えれば、ある距離で力が現れて横に移動することは期待できません。以下は、力線が外側に移動することを示す、より現実的な表現です。

同様に、ワイヤーのコイルからの力線も誤って表示されます。それらは、その中心に磁場が出現するものがない場合、コイルの中心から出現する磁力線を示します。この場合も、実際の磁場はコイル自体に由来する必要があります。これは、修正前と修正後の図です。

正味の力はそれが中心から来ているように感じるかもしれませんが、それは本当にその周りのワイヤーから来ています。電気コイルをペーパークリップの上に置く簡単な実験は、クリップがコイルの中心ではなく、コイルの端に引き付けられることを示しています。実際、大径のコイルの場合、中心での力は特に弱いです。
2020/04/19
オルタナティブフィジックス①
電気的地球科学では電気力線はまっすぐに対象に届くと考えている。これと同じ考えをする研究者が海外にいたので紹介したい。Bernard Burchell博士のAlternative Physicsから、Electric Fieldsを抜粋で紹介しよう。翻訳はグーグル先生です。
アナロジー
説明されている内容を視覚化するために、いくつかの類推を行うのが最善です。これについては、さまざまな考え方があります。1つは、(球形の)荷電粒子の表面から始まり、外側に広がる一連のゴム風船を想像することです。彼らがするように、彼らはますます伸ばされますが、決して破裂しません。
もう1つの方法は、粒子の細かい霧が外側にスプレーされることを想像することです。それらがそうであるように、それらの密度はますます密度が低くなります。つまり、より遠くのターゲットに当たる力が少なくなり、力が少なくなります。
これらのアニメーションは、意味が説明されているはずです。


上:「フィールドサブスタンス」を表す一連のゴム風船が荷電粒子の表面に形成されて外側に広がり、次第に薄くなっていますが、破裂することはありません。
下:小さな粒子が電荷内で生成され、光速で放出されています。
これらは単なる類似点です。おそらく、ゴムの連続的で無限に伸縮可能な塊を説明する方がより正確でしょう。しかし、それを描くのは難しい。
さまざまな理由から、小さな粒子で構成されるフィールドを想像する2番目の方法は、作業するのに最も便利なモデルです。それはそれが正しいことを意味するのではなく、電界と電荷の間の相互作用を想像する最も簡単な方法であるということだけです。このようにして、粒子をターゲットに力を及ぼす弾道発射物と見なすことができます。これから明らかな別のことは、粒子の密度が距離の2乗の逆数で減少するため、衝撃力がクーロン力と一致することです。これは、距離の2乗に伴って面積が増加する球の表面に均等に広がっているからです。
おそらく、この弾道粒子モデルの最も単純な直接的な類似は、太陽から来る太陽風と、風が「ソーラーセール」などのオブジェクトに力を及ぼす方法(まだ現実ではありません)でしょう。
フィールドライン
多くの場合、電界は、荷電粒子に出入りする線、および荷電粒子の周りを曲がる線によって記述および描画されます。このような図面は有用ですが、力の方向を示すための概念にすぎず、必ずしも物理的なものを表すものではないことを覚えておくことが重要です。残念ながら、これは私たちの分野の理解に大きな誤解をもたらしました。
次の電界図を検討してください。

この頻繁に引用されるプレゼンテーションは、正と負の電荷を示しています。電界は正の電荷から始まり、外側に移動します。左側は無料です。したがって、フィールドはほとんど直線で移動し(左端のラインは正確に直線です)、距離とともに徐々に弱くなります。右側は負の電荷です。したがって、フィールドはその電荷に向かって曲がり、その中に消えます。その間、負の電荷の右側には何もないので、フィールドはどこからでも現れ、その電荷に向かって移動しているように見えます。
この概念は確かに間違っています。電界は、電荷がそこに到達する前にその電荷がどこにあるのかわからないため、別の電荷に向かって曲がることができませんでした。私たちが歩くと、前方を見ることができ、その情報を使用して方向を決定できます。これは、視力が足よりもはるかに速いためです。しかし、電場はすでに軽い速度で移動しており、移動しているよりも速く「先を見る」ことができません。さらに、正負の区別は任意であるため、フィールドは両方向に実行されていることを示す必要があります。
この図には、イベントのより正確なバージョンがあります。

ここでは、両方の電荷がフィールドを生成し、両方のフィールドが電荷から直接離れて直線的に伸び、距離とともに弱くなっていることがわかります。前の図は、近くの個別の正電荷が経験する正味の力を説明している場合は正確である可能性がありますが、一般的な磁力線図ではありません。
力のモデリング
電界が荷電粒子に当たると、力がかかります。直感的なレベルでは、これは理にかなっています。空気の噴流などの物質を物体に吹き付けた場合、その物体に力が加わり、押しのけられます。
しかし、荷電粒子では力の方向は常に直感的ではありません。私たちが扱っている相互作用には2つのタイプがあります。同じような電荷間の反発力。反対の電荷間の引力。物事が「小さすぎて見えない」微視的レベルでどのように機能するかを理解しようとする場合、「日常世界」の巨視的レベルで物事と比較することは有用です。
反発力の場合、これは簡単です。荷電粒子から出現する小さな弾丸のストリームを想像してみてください。これらの弾丸はすべての方向から出現し、粒子から離れて直接軽い速度で移動します。近くにある同じように帯電した粒子は、これらの弾丸の力を感じ、弾丸によって反発されます。2番目の粒子が最初の粒子に近づくほど、弾丸がより多く弾丸に当たるため、力が大きくなります。粒子がさらに離れていれば、弾丸の数は少なくなり、力は小さくなります。
合わせて、速度依存クーロンの法則(VDCL)前に説明したように、粒子が内側に移動すると、弾丸の衝撃速度、つまり力が増加します。粒子が外側に移動すると、これにより衝撃速度と力が低下します。そして、その2番目の粒子が弾丸と同じ速度(つまり、軽い速度)で最初の粒子から離れた場合、弾丸はヒットせず、力をまったく加えることができません。
それでは、魅力的な力をどのように類推できるでしょうか?これも簡単に見えます。弾丸の方向を逆にして、荷電粒子に向かって内側に飛び込むようにします。残念ながら、その考えには大きな問題があります。弾丸が粒子に向かって移動するためには、粒子の位置だけでなくその速度も事前に知っている必要があります。弾丸は粒子を光速で打たなければならないので、彼らは粒子の速度を知る必要があります。弾丸はまた、宇宙の最遠端から時間の初めに出現し、どういうわけか逆の順序で他の粒子に影響を与える必要があります-つまり、最初に目的地に最も近い粒子に影響を与えます。これには、賢明な科学者が実現可能だと考えるレベルをはるかに超えるレベルの千里眼と逆タイムトラベルが含まれます。
電気力の新しいモデル
反対に帯電した粒子間の相互作用を説明するために、次のように電界と力を見ることができます。
各帯電粒子は、その電荷に対応するフィールドタイプを放出します。正に帯電した粒子は「正の電界」を放出し、負に帯電した粒子は「負の電界」を放出します。ただし、フィールド自体には料金は含まれず、発生元の料金に関する情報のみが含まれます。そのため、フィールドを「符号」を持つ、つまり正または負として表現できます。
これらのフィールドは、パーティクルのすべての「側面」から出現し、開始点に対して正確に軽い速度で外側に直接移動します。それらが別の粒子に出会うと、その粒子の電荷に応じて、フィールドの1つが押したり引いたりして相互作用します。
これらのフィールドはどのように相互作用しますか?プッシュプロセスの簡単なアナロジーは既にあるので、プルプロセスを見てみましょう。場は荷電粒子から発散し、軽い速度でそこから遠ざかります。反対に帯電した粒子に当たると、フィールドは突然「Uターン」し、その粒子を反対方向に押す、つまり引き寄せると見なすことができます。引っ張る動作は光速で起こり、その粒子は同じフィールドからの同じように帯電した粒子が受けるのと同じ(しかし反対の)力を受けます。この図はアクションを表しています。

類推として、パドルスチーマーを考えてみましょう。大きなボートが川に沿って蒸すと、そのパドルが手を伸ばし、水泳選手の手のように反対方向に水を引き出します。次に、この古いスタイルのボートに、ボートをどちらの方向にも動かすことができる最新の強力なプロペラエンジンが装備されていたとします。
プロペラがボートを後方に引くと、水に対するパドルの力が増加します。プロペラがゆっくりと前進すると、パドルの水に対する力が減少します。プロペラがパドルと同じ速度で押した場合、パドルは水に力を及ぼしません。そして、プロペラがさらに速く押すと、パドルは水を押し始めます。
わかりましたので、原子レベルでは弾丸やパドルスチーマーはありません。これらは、何が起こっているのかを視覚化するのに役立つモデルにすぎません。ただし、これには別のポイントがあります。特にプルフィールドUターンモデルは、次のセクションで使用されます。
------------------------------------------------------------
次に続きます。
2020/03/18
地球磁場と重力
人工衛星による地球磁場の測定がある。同じような人工衛星による重力測定では、衛星の軌道変化から重力の変化を推定していたのに対して、磁場は直接観測した値だ。地球磁場の分布をみると非常に興味深いことが見えてきた。

上の図は北大西洋の磁場の分布だ。下の図の重力分布と比較してみてほしい。重力分布は、地表と衛星の電荷による引力の変化だと指摘した。重力分布では海嶺から東西に延びる筋が磁場では垂直になっていることがわかる。

電子に力を加えると後方に円形磁場が発生する。地表近くの岩石に含まれた電子が自転方向に回転すると、角加速度で磁場が発生する。円形磁場は地表に現れると南北に向きがそろう。

電気的地球科学では、衛星軌道から見た重力は地下の岩石が蓄えている電子による電気引力だと主張している。磁場の観測からは分極した電荷を蓄えた岩石に対して直交した磁場が現われていることが分かった。これは電気的地球科学の地下275km付近に存在する膨大な電子が自転で回転することにより、磁場を発生させ、シューマン共振のELFで重力を発生させているとする主張を裏付けるものだ。
もし、ダイナモ理論が主張するように地球中心部のコアが磁場を発生させているとしたら、重力と磁場の分布がこれだけ相関関係を持っていることを説明できない。