Archives for: 2018年June
2018/06/21
中性子はなぜ崩壊する?②
中性子は陽子と電子が結合したものであるとした。同じ陽子と電子によって構成される水素原子がある。実際の水素原子は2個結合した分子だが、中性子と水素原子の質量は、こうなっている。有効桁は目をつぶってほしい。
中性子 n→ 1.674927471 x 10^-27kg
水素原子 H →1.6737236 x 10^-27kg
同じ陽子と電子でも、中性子のほうが少し重い。その差は、
n-H → 0.001203871 x 10^-27kg
となる。この差はなんだろう?
ところで、重水素は安定同位体で崩壊しない。
重水素 2H → 3.343583719 x 10^-27kg
重水素から、軌道電子1個と陽子2個の重さを引いてみる。
2H - e - 2p → 0.000749 x 10^-27kg
電子の重さは、
電子 e →0.00091093 x 10^-27kg
なので、ほぼ電子1個分の重さが出てくる。これが陽子と陽子を結合させている電子の重さなのだろうか?
そこで、三重水素と陽子3個の重さを比べてみた。
三重水素 3H →5.00827094 x 10^-27kg
軌道電子1個の重さを引く。
3H+ → 5.00736 x 10^-27kg
陽子3個は
3p → 5.017865484 x 10^-27kg
あれれ? 陽子3個のほうが重い!
3p - 3H+ → 0.010505484 x 10^-27kg
三重水素は、陽子が3個、電子3個で結合されていると考えられる。ではヘリウム3の重さはどうなっている?
3He → 5.00823789 x 10^-27kg
3He - 2e → 5.006416 x 10^-27kg
3H+ - 3He++ → 0.000944 x 10^-27kg
三重水素は、陽子3個が電子3個で、ヘリウム3は陽子3個が電子2個で結合している。その差は、ちょうど電子1個分になる。これは電気的地球科学で予想している原子核模型に合っている。三重水素はベータ崩壊するが、ヘリウム3は安定同位体だ。構造の違いは、三重水素が3角形をなしていて、ヘリウム3は真っ直ぐだ。
ここで、かなり飛躍的な予想をしてみる。

重水素は2個の陽子を電子が結び付けている。ニュートリノ放射を受けたとき、陽子内部で電界が伝わる。結合した電子を介してとなりの陽子にもニュートリノの電界は移動していく。このとき、電子を通り抜ける電界のパルスは真っ直ぐだ。ヘリウム3も陽子3個が直列につながっている。

三重水素でも陽子内部をニュートリノの電界のパルスは伝わるが、となりの陽子を結び付けている電子には角度がついている。そのため、電子内部には外側に向かう力が発生する。非常にエネルギーが高いニュートリノが入射した場合、電子を外側に弾き飛ばしてしまう。これがベータ崩壊だ。
ここまでくれば、中性子がなぜ崩壊するかは明らかだ。

陽子に入射したニュートリノが電子をはじき出してしまう。はじき出された電子はニュートリノのエネルギーを得て飛び去る。陽子が少し変形するので電子ニュートリノも発生する。
まだ、この考察には、なぜ3H<3pなのかという疑問もあるが、電界の再発生、ニュートリノによる電荷の供給という作用に矛盾はない。
うーん、しかしこれだと、①で予想したニュートリノの少ないほうが寿命が短いと矛盾する。困った。③へ続く。
2018/06/16
中性子はなぜ崩壊する?①
中性子は約15分で陽子と電子に崩壊するが、重水素は崩壊しない。三重水素は崩壊してヘリウム3になるが、半減期は12年だ。この違いはどこからくるのだろうか? 一般にはクォークで説明されているが嘘くさいので、別の仕組みを考えてみた。「素粒子宇宙起源研究機構」の中性子寿命の精密測定から、どのようにして中性子の寿命を測定しているかを見てみる。


グラフ1:2つの寿命測定法によるこれまでの測定値のズレ。青は超冷中性子蓄積実験、赤は冷中性子ビーム実験による値。線はそれぞれの実験の精度を考慮した平均値で、帯の幅は平均値の不確かさを表す。
いずれも速度の遅い中性子を使い、片方は容器に溜め、もう片方は一定の速度で検知器を通過させて測定している。容器に溜めたほうが寿命は平均8秒短い。寿命の差は、容器から漏れ出した可能性があるとしている。それにしても、8秒の差が明確にあるのは、何か原因があるからではないか?
以前、中性子の崩壊は、2個の中性子が結合するからではないかと説明した。この仕組みでは、ビームと容器での寿命の差は出ない。やはりニュートリノが関係していると思われる。

陽子に結合した電子は励起状態であると予想した。中性子は回転すると磁場を周囲に作る。磁場にエネルギーをとられるため、電子は次第に励起状態から電荷ポテンシャルが落ちていく。陽子にミューニュートリノがぶつかると一部のエネルギーが電子に渡り、電荷ポテンシャルを上げる。

中性子を容器に溜めた場合とビームにして測定した場合を比較してみる。容器に溜めた場合は、一定面積に一定時間ニュートリノが通り過ぎる。ビームの場合は速度に比例する。ニュートリノに放射される量はビームのほうが多いと考えられる。雨が降っているとき、立ち止まっているより、走ったほうが身体に当たる雨粒は多くなる。中性子も移動している場合のほうがニュートリノに当たる確率が高い。陽子に結合した電子の励起状態は、ニュートリノにより供給される電界のエネルギーによって維持されている、と予想できる。
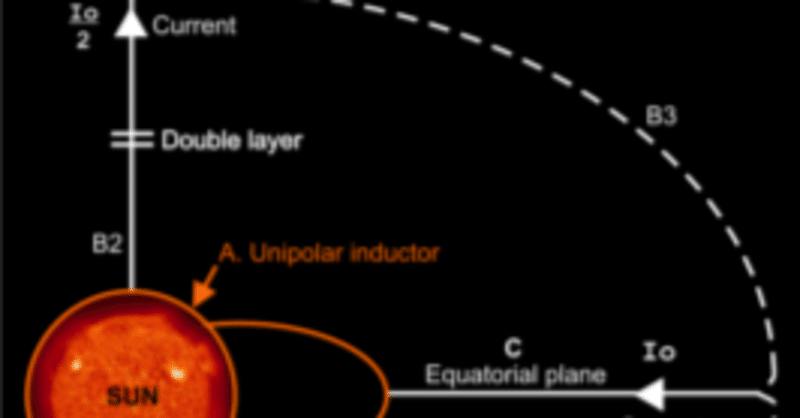
超高エネルギー宇宙線は超光速でやってくる
宇宙から大気に突入してくる宇宙線がある。宇宙線の多くは陽子が90%、ヘリウム原子核が9%を占めている。宇宙線はほとんどが10^18eV以下のエネルギーしか持たないが、まれに10^20~10^21eVのエネルギーを持つ超高エネルギー宇宙線(ultra-high-energy cosmic ray)が観測される。
たとえば、陽子が1個、光速で飛んでいる場合のエネルギーは次のように計算される。
E = 1/2mv^2
m = 1.67x10^-27 , c = 2.99 x 10^8m/s
E = 0.5 x 1.67x10^-27 x (2.99 x 10^8)^2
= 0.75 x 10^-10J
1J = 6.241 x 10^18eV
E = 4.68 x 10^8eV
これは運動エネルギーなので、陽子自体が持つ電荷は含まれない。陽子1個が大気に飛び込んでくると、酸素原子、窒素原子などに衝突して、さまざまな粒子が生じて地表に降り注ぐ。1個の陽子から1000億個の粒子が発生するといわれる。

空気シャワー、proton shower という。大量に発生する粒子は、パイ中間子、ミュー粒子、中性子、電子のほか、ミューニュートリノ、電子ニュートリノなどがある。
ところで、宇宙線の中には10^18eVより大きなエネルギーを持つ超高エネルギー宇宙線と呼ばれる非常にエネルギーの高いものがある。とくに5x10^19eVより大きなエネルギーを持つ最高エネルギー宇宙線 (EECR)の存在がある。
EECRは「2004年から2007年にかけて行われたピエール・オージェ観測所(英語版) (PAO) での最初の観測で、5.7×10^19eV を超えるものは27回しか観測されなかった。これは、3,000km2もの面積を持つ観測所で4週間に1度程度しか観測されないという少なさである」wikipedia
たとえば、光速の1000000倍の速度で突入する陽子は、どれくらいのエネルギーを持つだろうか? 最初の式で計算すれば次のようになる。
E = 4.68 x 10^20eV
これはEECRそのものだ。相対性理論を信じるなら、光速を超える粒子は存在しない。光速に近づくと質量が増えていって、加速されないからだ。EECRの発生源は、超新星爆発、ブラックホール周辺などが予想されている。しかし、星間物質の少ない宇宙空間では、ほとんどさえぎるものがない。相対性理論を無視すれば、荷電粒子は無制限に加速される。
太陽系外からの宇宙線は太陽磁場によって方向が変えられて、あまり多くは太陽系内には進入しない。さらに太陽系内部では、粒子が多いので、ぶつかる可能性が高くなる。地球近傍ではさらに粒子が増える。光速以上の速度を保ったまま大気に突入する宇宙線は、非常に少なくなると考えられる。
光速の10^6倍とはとんでもない速度なのだろうか? 天文学者・トム・フランデンによれば、重力の伝播速度は少なくとも光速の2x10^10倍だ。
電気的地球科学では、相対性理論を無視しているので、宇宙空間での速度制限はない。最高エネルギー宇宙線は、光速を超えてやってくる粒子だ。
追記:計算間違いが合ったので修正
2018/06/12
陽子と電子はなぜくっつかないか?
陽子はプラス、電子はマイナスの電荷を持つ。素電荷といって、陽子、電子の持つ電荷は、最初から備わっている性質と考えられている。ところがプラスとマイナスの電荷は、その距離により引き合う力が変わる。距離の二乗に反比例する。近づけば近づくほど電気引力は強くなる。
これが正しければ、陽子と電子は確実にぶつかるはずだ。ぶつかった状態がもっとも電気引力が強くなるので、結合する。太陽風は陽子と電子が混ざった状態のプラズマだ。太陽風は地球に来るまでの間に、陽子と電子が結合して中性子に変化するはずだ。しかし、太陽風の中には、ごくまれにしか中性子は観測されない。太陽風には陽子3個と電子2個で構成されるプロトン化水素が多く見られるだけだ。
陽子と電子は通常の状態ではくっつかない。通常の状態でないときにくっつくかといえば、常温核融合で中性子ができることが観測されている。電気放電、超音波振動を加えると、中性子が発生する。振動する原子核で指摘したが、原子核は励起状態でガンマ線を放射する。陽子1個でもガンマ線を放射している可能性がある。
陽子と電子が引き合う力はクーロン力だ。それぞれが持つ電界のエネルギーがクーロン力を生んでいるはずだ。マクロな系では、プラスとマイナスの電荷が近づくと、放電が起きる。完全にくっついてしまうと、電位差がなくなるので、クーロン力もなくなる。陽子と電子は素電荷なので、たとえくっついても電位差は保たれるのだろうか?もし、マクロな系と同じであれば、陽子と電子は近づくにつれて、電位差を解消する。加速されるので電磁波が放射される。近づけば近づくほど、電子は電荷がなくなり、クーロン力が低下して行って、距離がゼロではクーロン力もゼロになる。

陽子と電子が結合するためには、結合のためのエネルギーが必要になるはずだ。それがニュートリノではないか? 陽子に近づく電子がニュートリノの放射を受け、励起状態になると陽子に結合できる。

また、陽子がニュートリノを受けると陽子の電荷が変動して、電界が輻射される。電界の定在波が電子の接近を妨げる電界の谷間を作り出す。

陽子と電子が近づくとポテンシャルが低下してクーロン力が喪失する。電子がニュートリノを受け取り励起状態になると陽子と結合ができるので、中性子になる。通常は、陽子のほうが大きいため、ニュートリノの放射を受けやすい。ニュートリノにより励起されると陽子の電荷が増えるため、少し大きくなって電界の振動が起きる。電界の定在波(ガンマ線)が陽子の周囲に作られる。定在波のポテンシャルの谷間に電子が落ち込んで、陽子との衝突を避けている。(この定在波は電子軌道も作り出す)この3つの理由によって、陽子と電子はぶつかることがない。
2018/06/10
海面の変動と膨張の終焉
地球膨張はマントルのカンラン石が相転移して、体積が膨張するためだ。相転移に伴い二酸化炭素と水が生じる。
2SiO4 + CH4 -> 2SiO2 + CO2 + 2H2O
地球膨張は氷河期に急激に起こる可能性も指摘した。地球が膨張するため、海の面積が拡大する。海水が足りなくなるので、海水面は低下する。

Sea-level curve for the past 140,000 years, from Bard, et al., 1990.
氷河期に当たる7万年前から1万2千年前の間、海水面は低下していた。1万2千年ほど前から海水面の上昇が始まる。カンラン石の体積が膨張するために起こる海底の拡大と水の発生には時間差があるようだ。
日本では約8千年前に海面の急激な上昇、縄文海進があったがこのグラフでは誤差の中に埋まっている。14万年前から12万年まえにも海水面は急激に上昇している。リス氷期が終わった時期に相当している。
現在は次の氷期に向かう間氷期と考えられている。間氷期でも海水面は変動しているので、いずれ現在の海面も低下する可能性がある。カンラン石の膨張で発生した水の供給が減少するためだ。
問題は次の氷期がいつ始まるかだ。リス氷期とビュルム氷期の間には6万年の間氷期がある。これに従えば、あと4万5千年ほど間氷期は続く。しかしそれは、地球内部にまだ膨張していないカンラン石が残っているとしての仮定だ。もし、カンラン石が残っていない場合どうなるのだろう?カンラン石は水と二酸化炭素だけでなく電子も供給している。地下の電子は、自転、磁場、重力を生み出している。また、地球内部の空洞を電気的反発力で維持するという役目もある。カンラン石の枯渇は空洞の崩壊を意味する。つまり地球の寿命が尽きるのだ。